Túnel de Vento
EXPERIÊNCIA Nº 3 – DETERMINAÇÃO DO ARRASTO TOTAL SOBRE UM AEROFÓLIO EM TÚNEL DE VENTO
1. OBJETIVO
Determinar o arrasto total sobre um aerofólio com perfil simétrico padronizado denominado NACA0012 (NACA = National Advisory Committee for Aernautics, predecessor da NASA).
2. TEORIA
Um corpo de qualquer forma, quando imerso em um fluido em escoamento, está sujeito a forças e momentos (White, 1986). Estas forças são três: o arrasto, que age numa direção paralela à direção da corrente livre, e duas forças de sustentação, que agem em direções ortogonais. A atuação destas forças no corpo causa momentos, conforme ilustra a Fig.1.
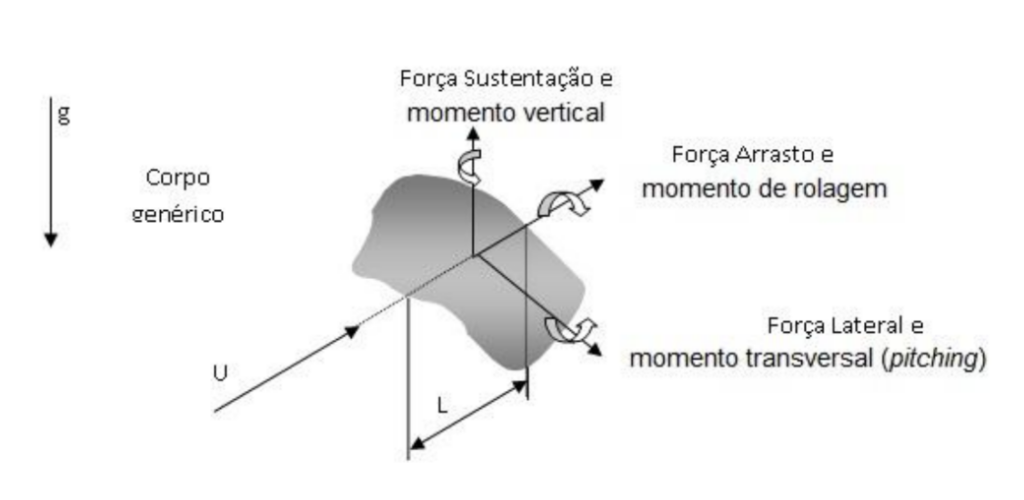
Figura 1. Forças e momentos atuantes em corpo genérico imerso num escoamento.
O experimento apresentado neste documento enfocará apenas a força de arrasto (D). Na sua forma adimensional, a força de arrasto é expressa pelo coeficiente de arrasto (CD), que é a razão entre D e uma força característica associada à pressão dinâmica da corrente livre, (1/2 ρU2), sendo ρ a densidade e U a velocidade da corrente livre.
O coeficiente de arrasto é expresso por:

O fator (1/2) é um tradicional tributo a Euler e a Bernoulli. A área característica do corpo (A) poderia ser igual a L2 (L é a dimensão linear característica do número de Reynolds), mas é usual encontrá-la definida como:
(i) A = Área Frontal – é a projeção da área em um plano perpendicular à direção da corrente livre (é a área “vista” pela corrente livre). É frequentemente utilizada para corpos ‘rombudos’ ou não-delgados, como esferas, cilindros, carros, mísseis, etc, ou
(ii) A = Área de Topo – é a projeção da área no plano paralelo à corrente livre (é a vista de topo). É utilizada para corpos delgados, como perfis de asa e hidrofólios, ou ainda,
(iii) A = Área Molhada – é a área total de contato do corpo com o fluido, costumeiramente utilizada para superfícies de cascos de embarcações.
Sabe-se que, em escoamentos com baixa velocidade, o coeficiente de arrasto de um corpo é uma função apenas do número de Reynolds (Re), ou seja,

O número de Reynolds é definido em termos da velocidade da corrente livre (U) e de um comprimento característico do corpo (L) conforme a Eq. (3). Esta dimensão característica do corpo pode ser a corda (dimensão transversal) ou o comprimento do corpo, medido em direção paralela à corrente livre.

A utilização de dados experimentais sobre arrasto ou outras forças exercidas pelo escoamento em corpos submersos pressupõe o conhecimento das dimensões linear e de área utilizadas no cálculo do número de Reynolds e do coeficiente de arrasto (isto é, estes valores são as escalas dos coeficientes medidos).
O arrasto exercido no corpo é composto pelas duas parcelas que aparecem na Eq. (4). O primeiro termo à direita do sinal de igualdade é o chamado “arrasto de atrito”, pois resulta da integração do produto entre o tensor das tensões viscosas, τW, que age na superfície, e a área superficial. A outra parcela, chamada de “arrasto de forma”, resulta da integração da pressão, p, que age sobre a superfície do corpo,

sendo dS o elemento de área na superfície do corpo e n a projeção, na direção do escoamento, do vetor unitário normal à superfície. Se dividirmos todos os termos da Eq. (4) pela força característica, obteremos uma expressão similar para o coeficiente de arrasto:

A determinação analítica ou numérica do arrasto, Eqs. (4) ou (5), ainda é um desafio à teoria da mecânica dos fluidos, exceto para uma placa plana ou corpos muito delgados. Isto se deve ao fenômeno da “separação do escoamento”. A teoria da camada limite pode determinar o ponto de separação, mas ainda não avalia satisfatoriamente a pressão (usualmente baixa) na região de separação. E mesmo a própria determinação do ponto de separação do escoamento pode ser comprometida. Por exemplo, a corrente que se descola do corpo na região de separação pode causar uma perturbação significativa no escoamento livre. Nestes casos, a teoria da camada limite pode ser aplicada somente se a distribuição de pressão no corpo for previamente conhecida (determinada experimentalmente, por exemplo). A Fig. 6 mostra as distribuições de pressão sobre um cilindro colocado transversalmente ao escoamento, de acordo com a teoria potencial, e valores medidos em escoamentos laminar e turbulento.
Em escoamentos subsônicos com número de Reynolds elevado (Re > 1000, por exemplo), o arrasto de forma pode superar em várias ordens de grandeza o arrasto de atrito. Entretanto, não se pode generalizar, pois a proporção dependerá da forma do corpo, isto é, se ela favorecerá ou não a separação hidrodinâmica.
Valores do coeficiente de arrasto para corpos com formas distintas, (a) cilindro, (b) cilindro com nariz arredondado, (c) cilindro com nariz arredondado e traseira delgada e (d) cilindro transversal ao escoamento, para escoamentos com ReL > 10000, estão na Fig. 2.
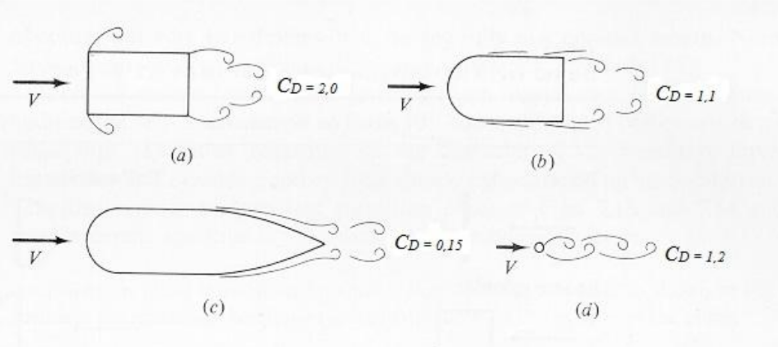
Figura 2. Coeficientes de arrasto para corpos de formas geométricas diferentes em escoamentos com ReL > 10000.
Em todos esses casos, a área característica para o cálculo do coeficiente de arrasto foi a área frontal do corpo. Observa-se que o coeficiente de arrasto para os corpos rombudos (não delgados), representados em (a), (b) e (d), tem valores entre 2,0 e 1,1. Já para o corpo com uma traseira delgada, que previne melhor a separação do escoamento, Fig. 2(c), há uma substancial redução do arrasto, isto é CD = 0,15! Isto é, se o cilindro da Fig. 2 (a) é a referência, nota-se que ao arredondar a frente do cilindro, Fig. 2(b),
reduz-se o arrasto em 45%; com a introdução de uma carenagem na parte traseira, entretanto, a redução do arrasto chega a 93%, Fig. 2(c).
A magnitude dos arrastos de forma e de atrito de um corpo delgado (streamlined) com razão de aspecto (t/c) variando entre 0,05 a 0,4, está mostrada na Fig. 3, onde t é a espessura do corpo e c é o comprimento da corda.
Para (t/c)→0 a forma do corpo aproxima-se de uma placa plana e o arrasto de atrito representa 83% do arrasto total. Por outro lado, quando (t/c) aumenta, isto é o corpo torna-se mais bojudo (arredondado), o arrasto de forma também aumenta.
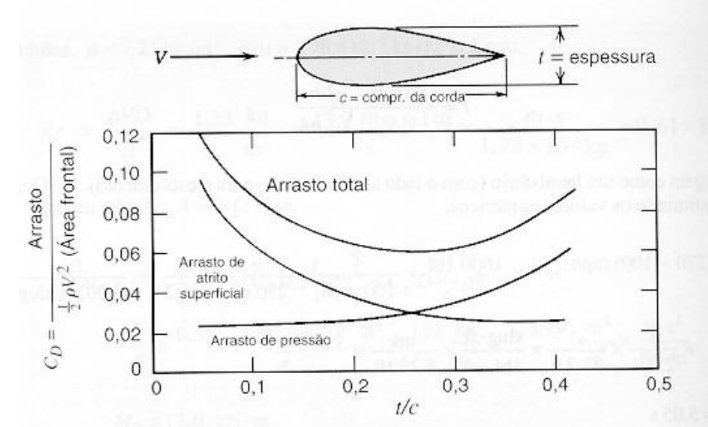
Figura 3. Influência do arrasto de atrito e de forma no arrasto total para um corpo delgado (carenado) em função da razão de aspecto (t/c).
Em corpos rombudos, isto é, não delgados, tais como cilindros e placas planas normais ao escoamento, o arrasto de pressão (ou seja, de forma) é dominante e corresponde a mais que 90% do arrasto total. Isto pode ser facilmente identificado se observamos a Fig. 4, que mostra CD em função do Re para corpos de formas variadas. Para escoamentos com Re > 1000, por exemplo, corpos delgados com formas de placas
planas, aerofólios, pássaros, etc, têm CD < 0,1. Nestes corpos, como visto na Fig. 3, os arrastos de forma e atrito são igualmente importantes na constituição do arrasto total. Por outro lado os corpos rombudos, como barra de seção quadrada, cilindro transversal ao escoamento e placa plana normal ao escoamento, têm CD ≈1.
A razão para os corpos rombudos apresentarem CD próximo da unidade é que a força de arrasto total é bem próxima do produto entre a pressão dinâmica e a área frontal.
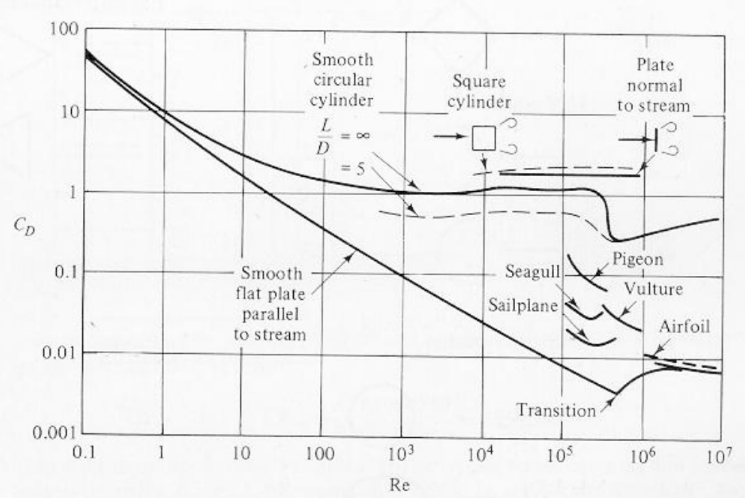
Figura 4. Coeficientes de arrasto para corpos bidimensionais em função do Reynolds.
De maneira aproximada pode-se estimar a força total de arrasto considerando que a diferença de pressão entre as superfícies do corpo, à montante e à jusante em relação ao escoamento, corresponde à pressão dinâmica, (1/2)ρU2, no ponto de estagnação frontal. Esta diferença de pressão vezes a área frontal do corpo [(1/2) ρU2 A] é, então, uma estimativa do arrasto total. Isto então justifica o fato, nestes corpos rombudos, do arrasto de forma ser a componente dominante no arrasto total.
Ainda com referência à Fig. 4, deve-se destacar um comportamento peculiar do CD do cilindro para números de Reynolds variando entre 105 e 106. Nesta faixa há uma súbita diminuição do CD de 1,2 para 0,3. Este fenômeno também é conhecido como “crise do arrasto” e deve-se a uma transição de regime laminar para turbulento da camada limite que se desenvolve na superfície do cilindro. Enquanto a camada limite laminar separa-se em uma posição angular de aproximadamente 82° a partir do ponto de
estagnação frontal, na camada limite turbulenta a separação ocorre em 120º, conforme mostrado na representação esquemática na Fig. 5. Na transição de laminar para turbulento, o escoamento na camada limite do cilindro consegue extrair mais energia do escoamento externo e retardar o ponto de separação para 120°.
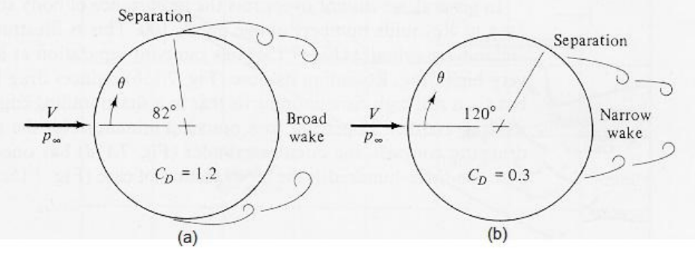
Figura 5. Representação esquemática do ponto de separação escoamento em um cilindro em regime laminar (a) e turbulento (b).
A redução do arrasto também pode ser observada na distribuição de pressão no cilindro para os diferentes regimes, como mostra a Fig. 6. CP é o coeficiente de pressão, P é a pressão sobre a superfície da esfera em Ɵ e P∞ é a pressão dinâmica no ponto de estagnação frontal. A curva tracejada é uma distribuição simétrica obtida da solução do escoamento potencial; as linhas ‘traço-ponto’ e ‘contínua’ são assimétricas e são valores medidos de escoamentos de camadas limites laminar e turbulenta. A assimetria na distribuição de pressão resulta, naturalmente, da separação do escoamento. A partir do valor máximo de estagnação frontal, o caso laminar apresenta uma pressão negativa e constante a partir de 82°. No caso turbulento o ponto de separação desloca-se para 120° e a distribuição de pressão é mais simétrica que a do caso laminar: portanto, o arrasto é menor.
Concluindo, por paradoxal que possa ser, a transição do escoamento de laminar para turbulento causa uma redução do arrasto total do cilindro. Sem dúvida, o arrasto de atrito aumenta quando o escoamento passa de laminar para turbulento. Porém, neste regime e para esta forma de corpo, a contribuição do arrasto de atrito para o arrasto total no cilindro é muito pequena quando comparado com o arrasto de pressão. Assim como a transição laminar-turbulento torna mais simétrica a distribuição de pressão, ela também reduz o arrasto total. A indução da transição laminar-turbulento passa então a ser um recurso empregado para redução de arrasto, neste caso específico.
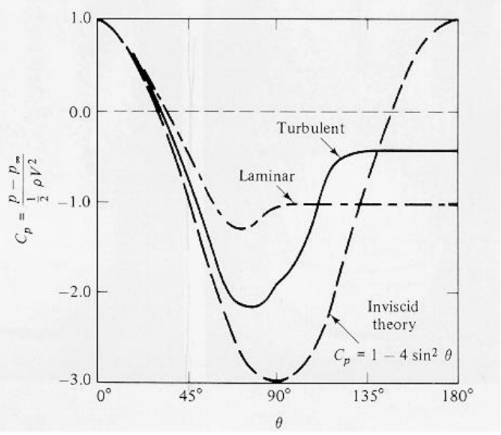
Figura 6. Distribuições de pressão num cilindro, causadas por um escoamento: potencial (teórico), camada limite laminar e turbulenta.
Na figura 6, CP é o coeficiente de pressão, P é a pressão sobre a superfície da esfera em Ɵ e P∞ é a pressão dinâmica no ponto de estagnação frontal.
A figura 7 mostra a visualização da entrada na água de duas bolas de boliche com 216 mm de diâmetro, a uma velocidade de 7,6 m/s (Re = 1,6 106).
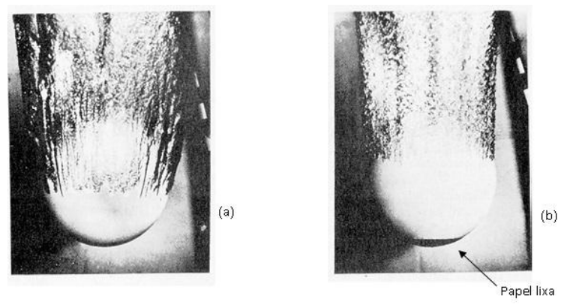
Figura 7. Diferenças entre os pontos de separação laminar (a) e turbulento (b) em uma bola de boliche de 216 mm de diâmetro entrando na água com 7,6 m/s.
Na figura (7a) o escoamento é laminar e o ponto de separação ocorre próximo ao equador da esfera. Na figura (7b), a mesma esfera, nas mesmas condições, tem o ponto de separação atrasado em relação ao caso (7a) devido à inserção de rugosidade causada por um papel lixa no nariz da bola. Uma mesma forma, porém em regime distinto, apresenta um arrasto diferente. Uma utilização popular do uso deste efeito para a redução de arrasto é a rugosidade criada na superfície das bolas de golfe.
3. SISTEMA EXPERIMENTAL
O arrasto total e o coeficiente de arrasto serão obtidos através da determinação do perfil de velocidades na esteira do perfil e da aplicação adequada das equações de conservação da massa e de quantidade de movimento linear, em conjunto com premissas simplificadoras apropriadas. O experimento será realizado em um túnel de vento sub-sônico (Fig. 8).

Figura 8. Fotografia do túnel de vento sub-sônico.
As medidas de velocidade serão obtidas por meio de medidores de Pitot, um localizado antes do aerofólio e outro localizado na região posterior ao aerofólio (bordo de fuga), conforme mostrado na Fig. 9.
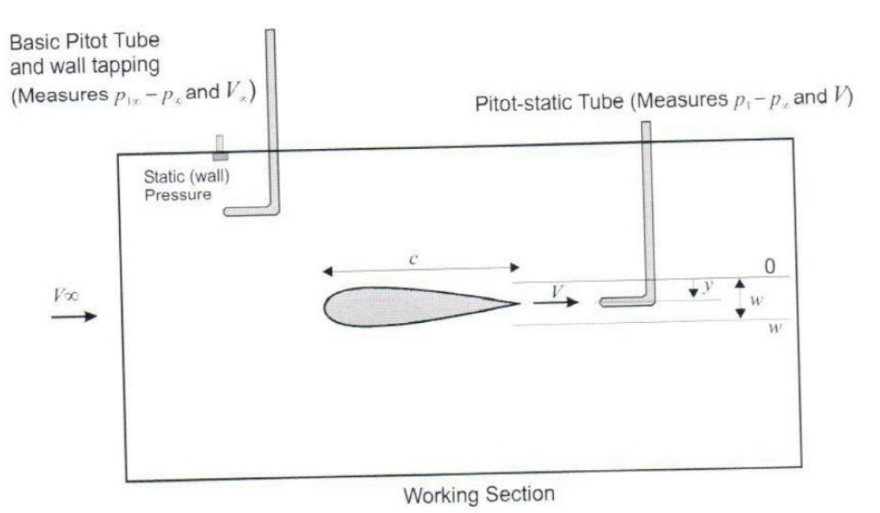
Figura 9. Esquema da seção de trabalho do túnel de vento.
3.1 Descrição qualitativa do escoamento
Nesta seção é realizada uma breve análise qualitativa do escoamento ao redor do perfil estudado. Devido às diferenças entre o escoamento à montante e à jusante do perfil, o campo de velocidades será dividido em duas regiões. Uma delimitada entre a região à montante do perfil (corrente livre, escoamento não-perturbado) até seu bordo de fuga; a outra, do bordo de fuga até uma certa distância à jusante, região conhecida como esteira. Por conveniência, elas passarão a ser denominadas por região do perfil e região da esteira, como indicado na Fig. 10a. Os perfis de velocidades nas regiões do perfil e da esteira estão representados esquematicamente também na Fig. 10a.
É possível notar que na região do perfil a presença da superfície sólida causa um retardo na velocidade devido ao não deslizamento do fluido. O escoamento próximo ao corpo sólido, devido o seu elevado Reynolds, caracteriza-se por um regime de camada limite. Definindo uma superfície de controle, SC (linha traço-ponto na Fig. 10a), cujos limites são demarcados por (0) e (1), e aplicando-se a conservação da massa no VC, observa-se que na região do perfil há uma expulsão de massa do VC devido à desaceleração do fluido. Por sua vez, na região da esteira, o perfil de velocidades é formado logo após o bordo de fuga do aerofólio, pela coalescência dos perfis de velocidade da parte superior e inferior.
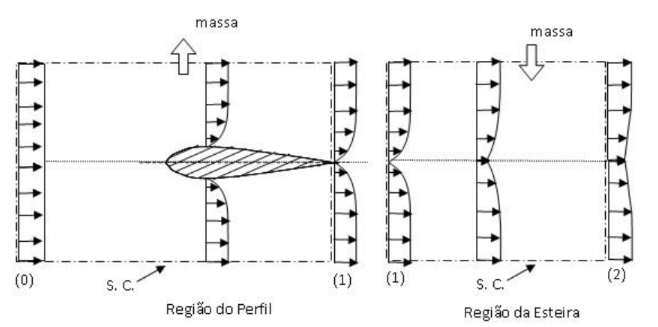
(a) Perfis de velocidades na região do perfil e na região da esteira

(b) presença da superfície sólida causa um retardo no perfil.
Figura 10. (a) Representação esquemática dos perfil a ser estudado e das superfícies de controle (0-1) e (1-2) para aplicação da equações apropriadas; (b) Visualização dos perfis de velocidade na esteira. Fluído: água, velocidade: 3,4 cm/s, espessura do perfil: 8 mm; Re = 280, técnica de visualização: bolhas de hidrogênio (Japan Society of Mechanical Eng., 1989).
A depressão que se visualiza na parte central do perfil de velocidades é resultante da desaceleração do fluído na região, causada por efeitos viscosos que ocorrem na camada limite. Este déficit de velocidade é recuperado à medida que o escoamento avança à jusante do corpo, como mostrado na Fig. 11.
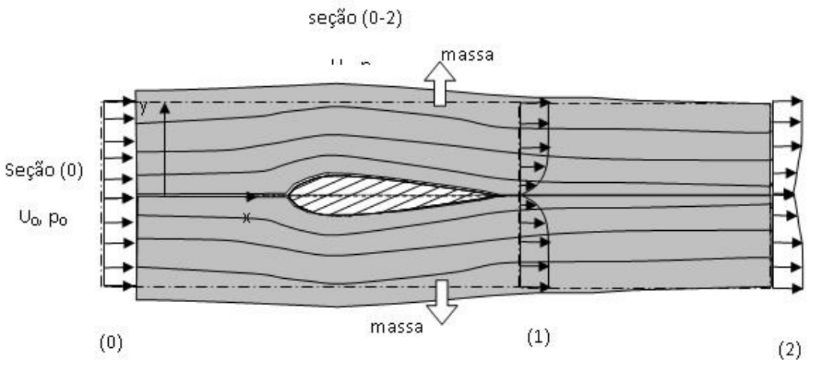
Figura 11. Definição das fronteiras da SC: seções (0), (2) e (0-2); dos perfis de velocidades nas seções (0), (1) e (2) e; dos tubos de corrente (fundo cinza claro).
Aplicando-se um balanço de massa no VC demarcado por (1-2) verifica-se um fluxo de massa do escoamento externo para o VC, conforme representado na Fig. 10a. O perfil de velocidades na esteira também é caracterizado por um escoamento de camada limite. Na visualização da Fig. 10b observa-se que o gradiente de velocidade na esteira não se estende por mais que duas vezes a espessura do aerofólio na direção transversal ao escoamento. Finalizando, espera-se que, se a seção (2) for posicionada muito afastada da seção (1) (bordo de fuga), o perfil em (2) será coincidente com o perfil em (0). Assim, a expulsão de massa na região do perfil será igualada ao fluxo do escoamento externo para o VC na região da esteira.
3.2 Método integral
O arrasto total exercido no perfil pode ser determinado experimentalmente através do cálculo da variação da quantidade de movimento linear do escoamento em um volume de controle que envolva o escoamento. O VC deve compreender desde a região à montante até a região da esteira do perfil. As equações básicas a utilizar são, então, as correspondentes ao balanço de massa e de quantidade de movimento. A equação de balanço de massa em regime permanente é expressa como:

Onde U é a velocidade do fluido que cruza a SC, n a sua normal e ρ a densidade do fluido. A equação integral da quantidade de momento, para regime permanente é:
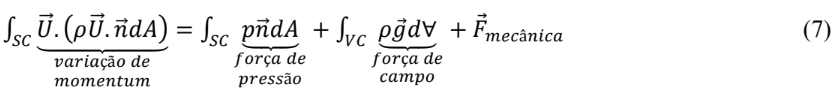
A equação (7) é de natureza vetorial e, portanto, compreende três equações escalares distintas correspondentes a cada direção de um sistema de eixos cartesiano. Considerando que o eixo x seja coincidente com a direção do fluxo de ar não perturbado (corrente livre), o arrasto total também coincide com esta direção, por definição. Assim, a ideia central para se determinar o arrasto total é determinar as componentes x das integrais que constituem o balanço de quantidade de movimento, Eq. (7). Para tanto, é necessário determinar experimentalmente os valores de velocidade e pressão que atuam na SC. O primeiro passo é a definição da SC. A Fig. 9 ilustra as fronteiras escolhidas para definir a SC. Ela é a forma retangular que envolve o perfil (linha traço-ponto). As seções (0) e (2) são a entrada e a saída da SC. Na seção (0) o fluxo é não perturbado e apresenta um perfil uniforme de velocidades. Na seção (2), longe o suficiente do bordo de fuga, o perfil apresenta ainda um déficit de velocidade, porém é quase uniforme. Podemos escolher a seção 2 como aquela de saída do túnel, onde a pressão também é p0. Assim, pode-se afirmar que tanto na seção (0) como na (2) a pressão estática é ‘praticamente’ p0, isto é, a pressão atmosférica, uma característica deste túnel de vento, especificamente, e também a pressão na corrente livre. Nas laterais da SC, seção (0-2), o escoamento está afastado, na direção y, do perfil de tal modo que as linhas de corrente apresentam uma curvatura quase nula, isto é, são ‘quase’ paralelas assim também pode-se afirmar que em (0-2) a pressão estática atuante é coincidente com p0. Nesta seção ainda há um fluxo de massa que cruza a SC (0-2) devido à desaceleração do fluido pelo perfil.
A escolha adotada para SC permite uma simplificação na forma da Eq. (7) para a direção (x). Observando-se que para a SC escolhida a pressão é uniforme e constante ao longo de todo o contorno, vem que a contribuição do termo de pressão é nula:

Já a força de campo é ortogonal à direção x. Consequentemente é nula, pois gx = 0:

Com isso, a componente na direção (x) da Eq. (7) é reduzida para dois termos, o balanço de quantidade de movimento e a força mecânica:

A força mecânica é uma força que cruza a SC, é a ação do perfil sobre o fluido (ou sobre o VC). Fisicamente, é a força mecânica exercida por um suporte onde o perfil está preso, suporte este que cruza a SC. Ela existe para manter o perfil estacionário, para que não seja carregado pela corrente de ar. O arrasto total, D, é a reação a esta força, isto é, a força que o fluido exerce no perfil. Assim, a relação entre a força mecânica e o arrasto total é:

E a forma final da Eq. (10) fica sendo:

A integral de superfície é avaliada nas quatro faces do SC:
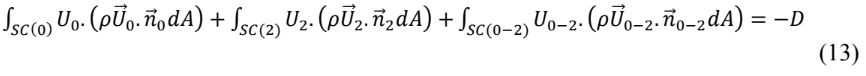
O terceiro termo à esquerda do sinal de igualdade é o fluxo de quantidade de movimento através de 0-2, isto é, o produto do fluxo de massa através de 0-2 com a velocidade naquela face. O fluxo de massa em 0-2 também é a diferença entre os fluxos de massa que entram e saem do VC. Ele é escrito por:

Se admitirmos agora que a componente na direção x da velocidade U na seção (0-2) coincide com a velocidade da corrente livre, isto é U0-2,x = U0 , podemos substituir a Eq. (14) em (13) para chegar a:
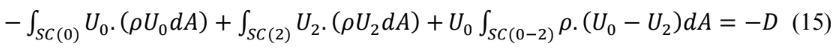
Agrupando e simplificando os termos da equação (15) tem-se que:

Vale lembrar que, para o perfil bidimensional em questão, o elemento de área, dA, é o produto do diferencial de altura, dy, e a largura b do perfil. O arrasto total fica então sendo:

Onde +y0 e –y0 são as posições verticais superior e inferior do escoamento na esteira, no limite da ocorrência do escoamento não perturbado. A Eq. (17) mostra que o produto entre a diferença de velocidade (U0 – U2) com o fluxo de massa na seção (2) resulta no arrasto total exercido pelo perfil no corpo.
3.3 Método de Jones
Apesar da equação (16) ser correta, ela não é factível de aplicação para se determinar experimentalmente o arrasto (pelo menos com a instrumentação de que dispomos). Na seção (2) o perfil de velocidades já se recompôs e a velocidade U2 já é muito próxima de U0, induzindo uma elevada incerteza na medição da diferença (U0 – U2).
O método de Jones (SCHLICHTING, 1968) propõe duas modificações que permitem a determinação do arrasto total, conforme Eq. (17), porém com os valores experimentais medidos na seção(1) (1), evitando assim as incertezas resultantes da diferença (U0 – U2).
As modificações são:
1) O fluxo de massa(2) ao longo de um tubo de corrente entre as seções (1) e (2) na Fig. 9, relaciona as velocidades U1 e U2 :

2) Segundo o método de Jones, o escoamento ocorre sem perdas entre as seções (1) e (2), isto é, a pressão total PT permanece constante(3) ao longo de cada tubo de corrente entre as seções (1) e (2):

| (1) Ao se adotar a seção (1) para medição tem que se assegurar que a vazão expulsa pela face (0-2) da SC na seção (1) seja coincidente com aquela determinada na seção (2). (2) A escolha da SC indicada na Fig. 10 garante que a vazão mássica expulsa na seção (2) possa ser calculada por meio das medidas na seção (1). A Eq. (14) modifica-se para: 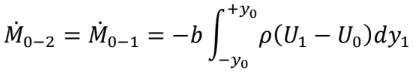 e a Eq. (15) para: 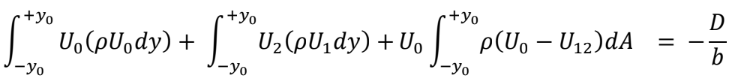 Deve-se destacar que o fluxo de momento na seção (2) é calculado a partir da vazão mássica em (1) pela velocidade em (2). A equação acima tem a mesma forma da Eq. (21). (3) A equação de Euler ao longo de uma linha de corrente assegura que para cada linha de corrente PT se conserva, PT,1 = P T,2. Assim sendo, a velocidade U2 é determinada pela Eq. (22). |
A pressão total é definida como a soma das pressões estática e dinâmica do escoamento e, para cada plano, são definidas por:



Substituindo a Eq. (18) na Eq. (17):

Utilizando as Eqs. (20a) e (20b), é possível escrever as velocidades U0, e U1 como:

Onde ΔP1 e ΔP2 referem-se às medidas de pressões dinâmicas fornecidas pelos medidores de Pitot antes e após o aerofólio, respectivamente.
Utilizando a Eq. (22) é possível escrever a Eq. (21) em função das pressões manométricas lidas diretamente pelos tubos de Pitot, isto é,
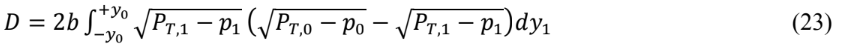
Ou, expressando o arrasto na forma do coeficiente de arrasto, conforme definido pela Eq. (3),
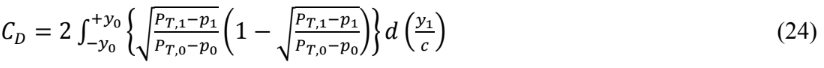
O cálculo deste CD baseia-se na área de topo do aerofólio, A = L∙c, onde L e c são, respectivamente, a Largura (300 mm) e a corda (152,4 mm) do aerofólio. Portanto, A = 0,04572 m2.
Tanto a Eq. (23) quanto a Eq. (24) devem ser integradas ao longo de toda a seção (1). Em ambos os casos o integrando difere de zero somente na porção da região 1 onde existe diferença de velocidade na esteira. A Eq. (23) transforma-se na Eq. (17) quando a pressão estática na seção (1) for igual a pressão estática da corrente livre, p1=p0.
3.4 Implementação numérica
A equação (24) é a equação de trabalho que permitirá calcular o coeficiente de arrasto do perfil. Para diferentes posições ao longo do eixo y, deverão ser determinadas as diferenças de pressão indicadas na equação. Depois será calculado o integrando da equação para cada ponto de medida. Teremos assim um conjunto de n pares de valores [i,(y/c)] onde i é dado pela Eq. (25):

Como as medições ao longo do eixo y serão discretas, deverá ser utilizado um procedimento de integração numérica, como a fórmula de Simpson:
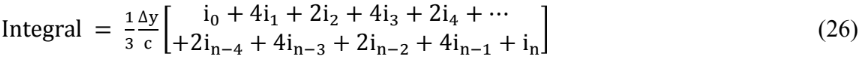
Onde Δy equivale ao passo, no caso Δy=1 mm, ik é o valor do integrando da Eq. (25) para o ponto de posição yk na seção (1) do túnel.
3.5 Descrição do aerofólio
Os equipamentos utilizados nesta experiência são o túnel de vento PLINT & PARTNERS, de seção quadrada de 300 mm e o aerofólio NACA 0012, de seção simétrica (Fig.12).
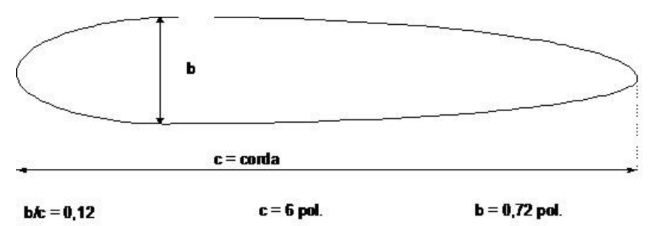
Figura 12. Dimensões do aerofólio NACA 0012, Largura de 300 mm.
b/c = 0,12 c = 152,4 mm b = 18,3 mm
4. PROCEDIMENTO EXPERIMENTAL
Etapa 1: Ligando o túnel de vento
- Ligue o isolador elétrico do painel de controle e instrumentação (botão power), girando-o no sentido horário.
- Ajuste o controle de velocidade (botão speed) no menor valor (completamente no sentido anti-horário).
- Pressione o botão verde START.
Obs.: Ao ligar o painel e pressionar o botão START, o ventilador pode levar alguns segundos para começar a trabalhar. A unidade de acionamento precisa de alguns segundos para energizar corretamente.
Etapa 2: Análise da influência da velocidade do escoamento de ar e do ângulo de ataque do aerofólio
- Inicialmente, ajuste o aerofólio para ângulo de ataque “zero” (posição horizontal da asa).
- Gradualmente, gire o controle de velocidade no sentido horário até o túnel funcionar na velocidade necessária para o experimento. Para a primeira velocidade, recomenda-se utilizar a velocidade máxima do túnel de vento (completamente no sentido horário). Ao alterar a velocidade, em uma segunda análise, recomenda-se reduzir pelo menos 30% em relação à velocidade anterior.
- Aguarde o sistema estabilizar.
- Ajuste a escala do medidor de Pitot (atrás do aerofólio – ΔP1 ), de modo que a leitura realizada corresponda a posição zero (posição central). Ou seja, inicialmente o Pitot deve estar posicionado na posição de menor velocidade.
- Ajuste a escala do medidor de Pitot localizado à frente do aerofólio (ΔP2) para a mesma posição do medidor de Pitot atrás do aerofólio (ΔP1) As medidas de ΔP1 e ΔP2 devem ser realizadas na mesma posição ao mesmo tempo. Sendo assim, as escalas devem ser ajustadas de maneira igual.
- Realize as tomadas de pressão ΔP1 e ΔP2 na posição central e, em seguida, em mais, pelo menos, 7 posições acima da posição central e 7 posições abaixo da mesma. Para cada posição, o valor fornecido para a força de arrasto deve ser anotado.
- Para a mesma velocidade, repita os procedimentos de 3 a 6, para uma nova inclinação de 5° do ângulo de ataque do aerofólio.
- Repita os procedimentos de 1 a 7 para uma nova condição de velocidade do ar.
Etapa 4: Desligando o túnel de vento
- Lentamente gire o controle de velocidade totalmente no sentido anti-horário.
- Pressione o botão vermelho STOP.
- Desligue o isolador elétrico do painel de controle.
5. APRESENTAÇÃO DOS RESULTADOS
1) Para as condições operacionais aplicadas, calcule a velocidade da corrente livre do ar (U0).
2) Calcule os números de Reynolds correspondentes às condições investigadas, utilizando a corda do aerofólio como dimensão característica.
4) Avalie as leituras das diferenças de pressão realizadas.
5) Trace as curvas do integrando em função da altura y [Eq. (25)], para as diferentes condições de operação no túnel.

6) Determine os coeficientes de arrasto para as condições de operação testadas calculando numericamente a integração indicada na equação (24) (método de Simpson). Compare com os valores obtidos a partir das medidas das forças de arrasto em cada condição operacional testada utilizando a Eq (1).
7) Discuta a influência do ângulo de ataque sobre os valores de CD obtidos.
8) Calcule a incerteza dos coeficientes de arrasto obtidos. Dado que o coeficiente foi calculado através de uma integração numérica e de uma equação, a incerteza pode ser obtida através do método de propagação de incertezas (erro provável). A incerteza na medida da coordenada “y” pode ser desprezada, já que se trata de um valor pré-fixado.
9) Procure na literatura valores do coeficiente de arrasto para o perfil NACA 0012 e compare com os resultados obtidos em suas medições.
6. REFERÊNCIAS BIBLIOGRÁFICAS
ABBOTT, I. H.; VON DOENHOFF, A. E. Theory of Wing Sections: Including a Summary of Airfoil Data. Dover Books, 1959.
FOX, R. W.; MCDONALD, A. T. Introdução à Mecânica dos Fluidos. Guanabara, 1981.
SCHLICHTING, H. Boundary Layer Theory. 2. ed. McGraw-Hill, 1968.
WHITE, F. M. Fluid Mechanics. 2. ed. McGraw-Hill, 1986.



