Impact Project fighting against underride: Forces

Follows the theoretical assessment of the forces arising during the impact of a car front end with the rear end of a truck equipped with a rigid underride guard.

The calculations presented here were based on the work of Prof. GEORGE RECHNITZER [1].

Centered impact

Assumptions:

both vehicles are traveling in the same straight trajectory;
the impact is essentially plastic;
no lateral displacement of the vehicles occurs after the impact;
after the impact both vehicles remain in contact as a single mass (m₁ + m₂) at speed v_3.

From the conservation of momentum:

m₁ v₁ + m₂ v₂ = (m₁ + m₂) v₃ (1)

v₃ = (m₁ v₁ + m₂ v₂)/ (m₁ + m₂) (2)

where:

m₁ = mass of the truck (kg)

m₂ = mass of the car (kg)

v₁ = velocity of the truck before impact (m/s)

v₂ = velocity of the car before impact (m/s)

v₃ = velocity of both vehicles after impact (m/s)

Before impact, the kinetic energy of the vehicles is:

E₀ = 0.5(m₁ v₁² + m₂ v₂²) (3)

And after impact:

E₁ = 0.5(m₁ + m₂)v₃² (4)

where:

E_n = kinetic energy (J)

The energy lost during impact is:

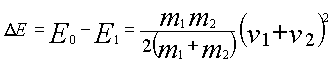(5)

Taking the closing velocity v_a = (v₁ + v₂), we obtain:

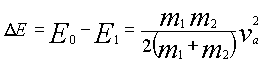(6)

The work done by the average force arising during the collision in crushing the car is:

F.s = D E = E₁ – E₂ (7)

where:

F = average force acting during the impact (N)

s = car crush (m)

and

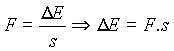(8)

Substituting eq. (8) in eq. (6), we obtain the average force acting between the vehicles during the impact:

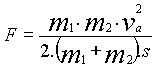(9)

Eq. (9) shows that the average force acting during the impact is function of the truck and car masses, closing speed and car crush distance (considering a rigid guard).

In order to verify the influence of the truck mass in the force acting during the impact, let us take three different kinds of cars ("small", "medium" and "large"). For each category we will consider two models, one produced in Brazil and one produced abroad. Crushing data for Brazilian models were obtained from a Brazilian industry which asked us not to divulge the names of its models. Crushing data for the foreign models were obtained at the NHTSA (National Highway Traffic Safety Administration) web site [2].

Table I presents the data employed to calculate the forces (crush distance for centered impact against rigid flat barrier).

TABLE I

Vehicle	mass (kg)	crush distance (m)	impact velocity (m/s)
Dahiatsu Charade	1,015	0.3861	13.33 (48 km/h)
Chevrolet Beretta	1,442	0.5105
Buick Century	1,749	0.587
Brazilian small car	1,100	0.511	13.89 (50 km/h)
Brazilian medium car	1,350	0.497
Brazilian large car	1,750	0.816

Table II shows the average force acting during impact calculated according eq. (9):

TABLE II

Truck mass (kg)	3,500	5,000	10,000	20,000	40,000
Dahiatsu Charade	181 kN	194 kN	212 kN	222 kN	228 kN
Chevrolet Beretta	178 kN	195 kN	220 kN	234 kN	243 kN
Buick Century	177 kN	196 kN	225 kN	244 kN	254 kN
Brazilian small car	158 kN	170 kN	187 kN	197 kN	202 kN
Brazilian medium car	189 kN	206 kN	231 kN	245 kN	253 kN
Brazilian large car	138 kN	153 kN	176 kN	190 kN	198 kN

Table II presents the average dynamic impact loads acting during the impact. Experimental results obtained by BEERMANN [3] show that the ratio of quasistatic crush loads to dynamic mean axial buckling loads for closed-hat section members (similar to front structural members of cars) ranges from 1.30 to 1.56 (average value = 1.40), with no influence of the speed within 30 to 50 km/h. Dividing the values of Table II by 1.40 we obtain the corresponding quasistatic crush loads that can be used for design purposes. These quasistatic loads are presented in Table III.

TABLE III

Truck mass (kg)	3,500	5,000	10,000	20,000	40,000
Dahiatsu Charade	129 kN	139 kN	151 kN	159 kN	163 kN
Chevrolet Beretta	127 kN	139 kN	157 kN	167 kN	174 kN
Buick Century	126 kN	140 kN	161 kN	174 kN	181 kN
Brazilian small car	113 kN	121 kN	134 kN	141 kN	144 kN
Brazilian medium car	135 kN	147 kN	165 kN	175 kN	181 kN
Brazilian large car	99 kN	109 kN	126 kN	136 kN	141 kN
Average	122 kN	133 kN	149 kN	159 kN	164 kN

According to the data presented in Table III, an underride guard able to resist an impact at 50 km/h of a hypothetical average car should be designed to resist the following quasistatic loads at the drop arm level (P₂):

TABLE IV

Truck mass	< 5 ton.	5-10 ton.	10-20 ton.	20-40 ton.
Quasistatic load to be applied at the drop arm level (P₂)	133 kN	149 kN	159 kN	164 kN

Offset impact

Unfortunately we were not able so far to get the crush data necessary to assess the force acting during an offset collision. So the assessment of these force will be based on the experimental results obtained by RECHNITZER et al. [4] e MARIOLANI et al. [5], who designed underride guards according to the quasistatic strength requirements proposed by BEERMANN [3], that is, 150 kN at the drop arm level (P₂) and 100 kN at the center of the main beam (P₃) and 300 mm from the outermost parts of the vehicle (P₁).
Both underride guard were successfully tested at 50 km/h, what allows one to suppose that the ratio of 1.5 between the load at the drop arm level and the load at the center of the beam and near its outermost part is satisfactory.
Based on this ratio (1.5) we suggest that underride guards should satisfy the following quasistatic strength requirements to be able to resist the impact of an AVERAGE car at 50 km/h:

Table V

Truck mass	< 5 ton.	5-10 ton.	10-20 ton.	20-40 ton.
Strength near the outermost part of the truck (P₁)	90 kN	100 kN	105 kN	110 kN
Strength at the drop arm level (P₂)	135 kN	150 kN	160 kN	165 kN
Strength at the center of the main beam (P₃)	90 kN	100 kN	105 kN	110 kN

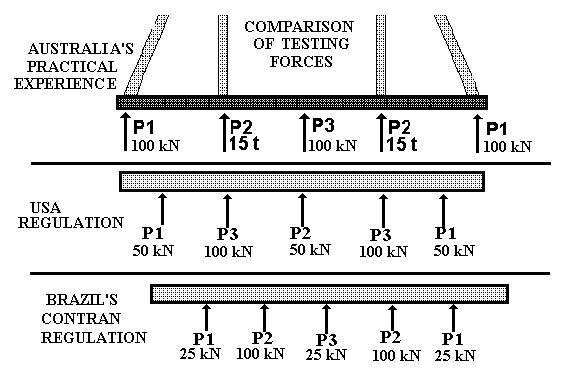
Example of "half safety"

Comparing the guard strength suggested above with the test forces required by the new American and the Brazilian (= European) standards, we can easily conclude that the traffic authorities do not know what a collision means...

References

RECHNITZER, G. – "Design Principles for Underride Guards and Crash Test Results". Notes for SAE Heavy Vehicle Underride Protection TOPTEC, April 15-16 1997, Palm Springs, USA.
NHTSA (National Highway Traffic Safety Administration) Vehicle Crash Test Data Base. URL: http://www-nrd.nhtsa.dot.gov/database/nrd-11/veh_db.html
BEERMANN, H.J. – "Behaviour of Passenger Cars on Impact with Underride Guards". Int. J. of Vehicle Design, vol. 5, nos. 1/2, pp. 86-103, 1984.
RECHNITZER, G.; SCOTT, G. & MURRAY, N.W. – "The Reduction of Injuries to Car Occupants in Rear End Impacts with Heavy Vehicles". SAE Paper 933123. 37^th Stapp Car Crash Conference Proceedings, San Antonio, Texas, USA, November 8-10, 1993.
MARIOLANI, J.R.L.; ARRUDA, A.C.F; SANTOS, P.S.P; MAZARIN, J.C. & STELLUTE, J.C. – "Design and Test of an Articulated Rear Guard Able to Prevent Car Underride". SAE Paper 973106. VI International Mobility Technology Conference and Exhibit, São Paulo, Brasil, October 27-29, 1997.