EM435 - Introdução à Engenharia de Fabricação
Gabarito da primeira prova - 07/10/1998
Questão 1) O conceito de linha de montagem, tal como concebemos nos dias de hoje, só foi possível graças ao conceito anterior de intercambiabilidade. O que é este conceito, qual a sua relação com os conceitos de precisão (do produto) e limites de tolerância, e como este conceito possibilitou o projeto para a manufatura?
O conceito de intercambiabilidade foi utilizado inicialmente no século XVII na indústria bélica européia e, a partir do início deste século, de forma mais ampla na indústria automobilística por Henry Ford. Intercambiabilidade pode ser entendida como a possibilidade de montar-se um conjunto mecânico a partir de peças retiradas aleatoriamente de lotes diversos de fabricação sem a necessidade de ajustagens posteriores, garantindo a funcionalidade e a qualidade do conjunto montado.
Os componentes fabricados e os conjuntos montados devem apresentar uma dada precisão em função das exigências de sua utilização. Essa precisão está associada a limites de tolerância, tanto mais próximos quanto maior for a qualidade (precisão) exigida. Deve-se destacar que existe uma forte dependência entre custo e qualidade, que deve ser analisada em função da competitividade esperada para esses produtos no mercado consumidor.
O conceito de um produto projetado para a manufatura foi introduzido por Ford em seu modelo T em 1908, quando as condições de fabricação e montagem permitiram que se aplicasse plenamente o conceito de intercambiabilidade e se implantasse a linha de montagem com todas as vantagens decorrentes em relação à produção artesanal. Por esse conceito, os componentes são projetados já considerando as variações toleráveis para suas dimensões e geometria e também, considerando os processos de fabricação disponíveis.
Questão 2) Com base nas tabelas A.2.1 e A.3.2 determinar: a) quais os afastamentos superiores e inferiores dos furos e eixos; b) quais as tolerâncias e qualidades de trabalho; c) qual o tipo de ajuste e d) quais as folgas/interferências máximas e mínimas.
| Ajuste |
As |
Ai |
as |
ai |
tfuro |
ITfuro |
teixo |
ITeixo |
tipo |
Fmax |
Fmin |
Imax |
Imin |
| 60H8/d7 |
46 |
00 |
-100 |
-130 |
46 |
8 |
30 |
7 |
folga |
176 |
100 |
- |
- |
| 30H6/k5 |
13 |
00 |
11 |
02 |
13 |
6 |
09 |
5 |
incerto |
11 |
- |
11 |
- |
| 50M8/h7 |
05 |
-34 |
00 |
-25 |
39 |
8 |
25 |
7 |
incerto |
30 |
- |
34 |
- |
| 40H6/r5 |
16 |
00 |
45 |
34 |
16 |
6 |
11 |
5 |
interfer. |
- |
- |
45 |
18 |
| 180F5/h4 |
61 |
43 |
00 |
-12 |
18 |
5 |
12 |
4 |
folga |
73 |
43 |
- |
- |
| 45H8/c7 |
39 |
00 |
-130 |
-155 |
39 |
8 |
25 |
7 |
folga |
194 |
130 |
- |
- |
| 70H7/j6 |
30 |
00 |
12 |
-07 |
30 |
7 |
19 |
6 |
incerto |
37 |
- |
12 |
- |
| 80P7/h6 |
-21 |
-51 |
00 |
-19 |
30 |
7 |
19 |
6 |
interf. |
- |
- |
51 |
2 |
| 35H8/u7 |
39 |
00 |
85 |
60 |
39 |
8 |
25 |
7 |
interf. |
- |
- |
85 |
21 |
| 15G5/h4 |
14 |
06 |
00 |
-05 |
08 |
5 |
05 |
4 |
folga |
19 |
06 |
- |
- |
| 60H11/h11 |
190 |
00 |
00 |
-190 |
190 |
11 |
190 |
11 |
folga |
380 |
00 |
- |
- |
| 50H7/m6 |
25 |
00 |
25 |
09 |
25 |
7 |
16 |
6 |
incerto |
16 |
- |
25 |
- |
| 25N8/h7 |
-03 |
-36 |
00 |
-21 |
33 |
8 |
21 |
7 |
incerto |
18 |
- |
36 |
- |
| 70H8/t7 |
46 |
00 |
105 |
75 |
46 |
8 |
30 |
7 |
interf |
- |
- |
105 |
29 |
| 40G6/h5 |
25 |
09 |
00 |
-11 |
16 |
6 |
11 |
5 |
folga |
36 |
09 |
- |
- |
| 30H10/e9 |
84 |
00 |
-40 |
-92 |
84 |
10 |
52 |
9 |
folga |
176 |
40 |
- |
- |
| 75H7/j6 |
30 |
00 |
12 |
-07 |
30 |
7 |
19 |
6 |
incerto |
37 |
- |
12 |
- |
| 110K8/h7 |
16 |
-38 |
00 |
-35 |
54 |
8 |
35 |
7 |
incerto |
51 |
- |
38 |
- |
| 35H7/s6 |
25 |
00 |
59 |
43 |
25 |
7 |
16 |
6 |
interf. |
- |
- |
59 |
18 |
| 60G7/h6 |
40 |
10 |
00 |
-19 |
30 |
7 |
19 |
6 |
folga |
59 |
10 |
- |
- |
Questão 3) O que são os gráficos de controle estatístico de processos (CEP), como são obtidos e para que servem? Quais são os princípios que fazem com que seja possível analisar a evolução de um processo qualquer através destas cartas de controle?
Os gráficos de controle estatístico de processos são representados pelas cartas de controle, pelos histogramas e pelas curvas de distribuição normal que caracterizam esses processos. A carta de controle é talvez o gráfico mais importante pois a partir dela pode-se obter os outros dois gráficos.
A carta de controle é obtida a partir da medição de uma dada variável empregando-se amostras que representam os lotes produzidos. O eixo das ordenadas representa os valores médios obtidos nessas amostras e no eixo das abscissas apresenta-se o número das amostras. Na carta de controle também especificam-se os limites de controle que indicam a variabilidade do processo analisado.
Os gráficos de controle estatístico fornecem resultados úteis para avaliar-se a capacidade e a capabilidade do processo estudado, determinando-se sua variabilidade e se está ou não ajustado.
Um processo somente pode ser avaliado estatisticamente se todas as variáveis com causas identificáveis já estiverem eliminadas, estando somente sob efeito das variáveis aleatórias. Pressupõe-se que o processo analisado apresente-se como uma distribuição normal estável com média e desvio-padrão constantes.
Questão 4) Qual a diferença básica entre o índice de capacidade de processo Cp e o índice de capacidade real de processo Cpk (ou índice de Capabilidade de processo)? Como aplicar ambos os conceitos?
O índice de capacidade de processo Cp é empregado para medir a variabilidade do processo, ou seja a dispersão dos valores medidos para a variável sob controle. Um processo é definido capaz quando seu desvio-padrão é menor que um oitavo da tolerância especificada e que somente 0,27% das peças produzidas sejam defeituosas, determinando um valor de Cp maior ou igual a 1,33.
Já o índice de capacidade real do processo Cpk (ou índice de capabilidade) além de indicar a dispersão verificada no processo, também permite avaliar-se se o processo está centrado em torno da média. Um processo que apresenta Cpk maior ou igual a 1,33 apresenta-se capaz e com boa capabilidade, sendo que esse processo estará ajustado se apresentar valores de Cpk1 e Cpk2 iguais.
Assim, Cp permite verificar se o processo é adequado para obter-se a tolerância desejada e Cpk define se o processo precisa ou não ser ajustado para apresentar-se centrado em relação à média esperada.
Questão 5) Interpretar para as peças abaixo todas as indicações existentes.

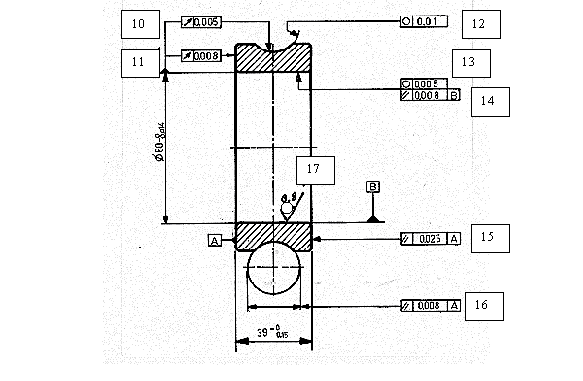
- A superfície indicada deve apresentar uma leitura indicada total no batimento radial de no máximo 0,012 mm em relação à superfície superior do furo de diâmetro nominal 80 mm
- A superfície indicada deve apresentar uma leitura indicada total no batimento axial de no máximo 0,005 mm em relação à superfície superior do furo de diâmetro nominal 80 mm
- A superfície indicada deve apresentar um erro de perpendicularismo de no máximo 0,015 mm em relação à superfície superior do furo de diâmetro nominal 80 mm
- A linha indicada deve apresentar um erro máximo de retitude igual a 0,02 mm
- A superfície deve apresentar na região indicada, um erro máximo de circularidade igual a 0,006 mm
- A superfície indicada deve apresentar um erro máximo de paralelismo igual a 0,005 mm em relação à superfície de referência A
- A superfície indicada deve apresentar um erro máximo de paralelismo igual a 0,01 mm em relação à superfície de referência B
- A superfície deve apresentar na região indicada, um erro máximo de circularidade igual a 0,008 mm
- A superfície indicada deve apresentar um valor de Ra = 0,3 mm e a remoção de material é exigida
- A superfície indicada deve apresentar uma leitura indicada total no batimento radial de no máximo 0,005 mm em relação à superfície superior do furo de diâmetro nominal 80 mm
- A superfície indicada deve apresentar uma leitura indicada total no batimento axial de no máximo 0,008 mm em relação à superfície superior do furo de diâmetro nominal 80 mm
- A superfície deve apresentar na região indicada, um erro máximo de circularidade igual a 0,01 mm
- A superfície deve apresentar na região indicada, um erro máximo de circularidade igual a 0,005 mm
- A superfície indicada deve apresentar um erro máximo de paralelismo igual a 0,008 mm em relação à superfície de referência B
- A superfície indicada deve apresentar um erro máximo de paralelismo igual a 0,025 mm em relação à superfície de referência A
- A superfície indicada deve apresentar nos locais indicados (arco de contato) um erro máximo de paralelismo igual a 0,008 mm em relação à superfície de referência A
- A superfície indicada deve apresentar um valor de Ra = 0,8
mm e a remoção de material não é permitida


